Kernels for LayerNorm forward pass
Introduction
The Layer Normalization (LayerNorm) operation applies normalization across the last D dimensions of the activation tensor as described in this foundational paper by Ba et al. (2016). The normalization equation is given below:
$$y = \frac{x - \mathbb{E}[x]}{\sqrt{Var[x] + \epsilon}} \times \gamma + \beta$$
where, \(\mathbb{E}[z]\) and \(Var[z]\) are the expectation and variance of random variable \(z\), respectively. Note that in the above \(\epsilon\) is a small term for to avoid division by zero errors, whereas \(\gamma\) and \(\beta\) are scale and shift parameters, respectively.
This pocket reference outlines and provides a detailed explanation of a series of CUDA kernel implementations of LayerNorm forward pass based on the llm.c github repository. Please refer to the Layer Normalization pocket reference for conceptual understanding and other details about the operation. For the purpose of this pocket reference, lets implement kernels for LayerNorm in the Transformer architecture for language modeling. The input to the LayerNorm operation is expected to be a tensor of shape \((B, T, C)\) as input, where:
- \(B\) is the batch size
- \(T\) is the sequence length
- \(C\) is the hidden dimension size.
LayerNorm is applied along the last dimension \(C\). For benchmarking purposes, we use the following configuration:
- \(B = 8\)
- \(T = 1024\)
- \(C = 768\)
The following table shows memory bandwidth for each kernel on a A40 GPU for block size 512. The last column shows improvement over the first kernel:
| Kernel # | Bandwidth (GB/s) | Improvement |
|---|---|---|
| 1 | 41.43 | - |
| 2 | 201.25 | 4.9x |
| 3 | 362.10 | 8.7x |
| 4 | 432.03 | 10.4x |
| 5 | 538.88 | 13x |
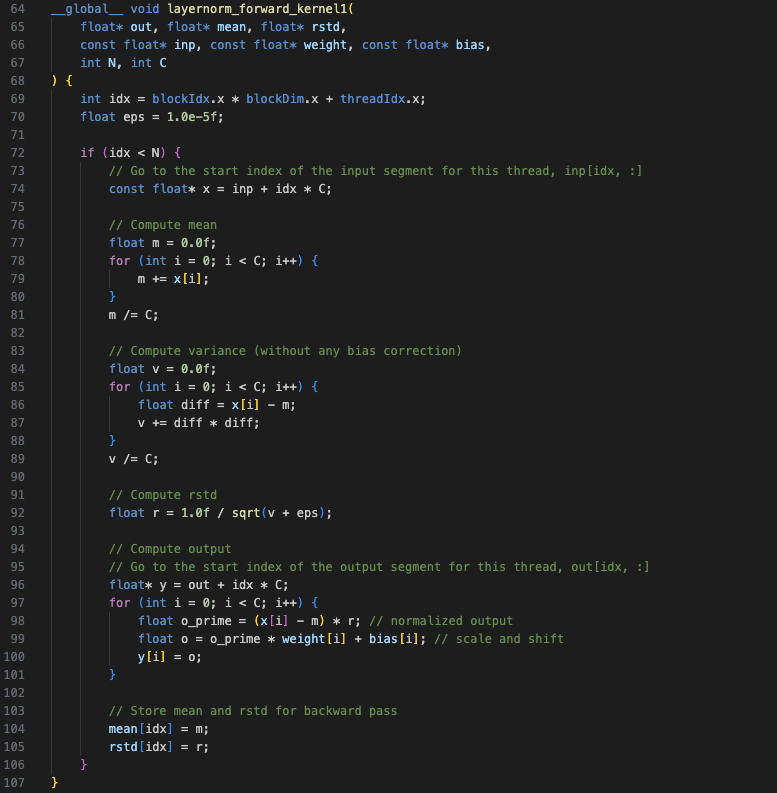
Kernel 1
The first kernel is a copy of the CPU implementation. It parallelizes over the first 2 dimensions, \(B\) and \(T\), where \(N = B*T\). A single thread (see Figure-1a) is responsible for normalizing one segment of size C, hence it loops over all elements in that segment. The kernel code is broken down into 4 steps:
-
Mean calculation
$$\mathbb{E}[x] = \frac{1}{C} \sum_{i=1}^{C} x_i$$
-
Variance and reciprocal of standard deviation (rstd) calculation
$$Var[x] = \frac{1}{C} \sum_{i=1}^{C} (x_i - \mathbb{E}[x])^2$$
$$rstd[x] = \frac{1}{\sqrt{Var[x] + \epsilon}}$$
-
Apply mean and variance normalization and then scale and shift with the learnable weight and bias parameters
$$y_i = ((x_i - \mathbb{E}[x]) * rstd[x]) * \gamma_i + \beta_i$$
-
Store mean and rstd for backward pass
The kernel uses a 1D grid and block as shown in Figure-1a. Also note that all operations are implemented in a single kernel.

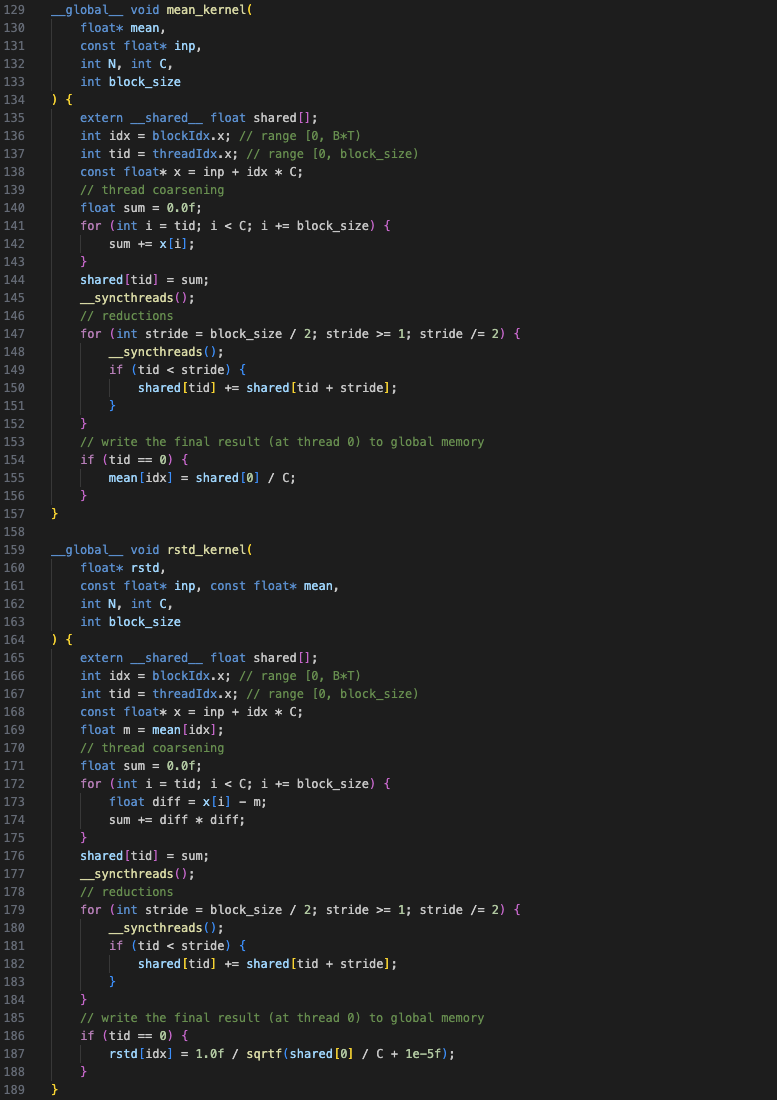
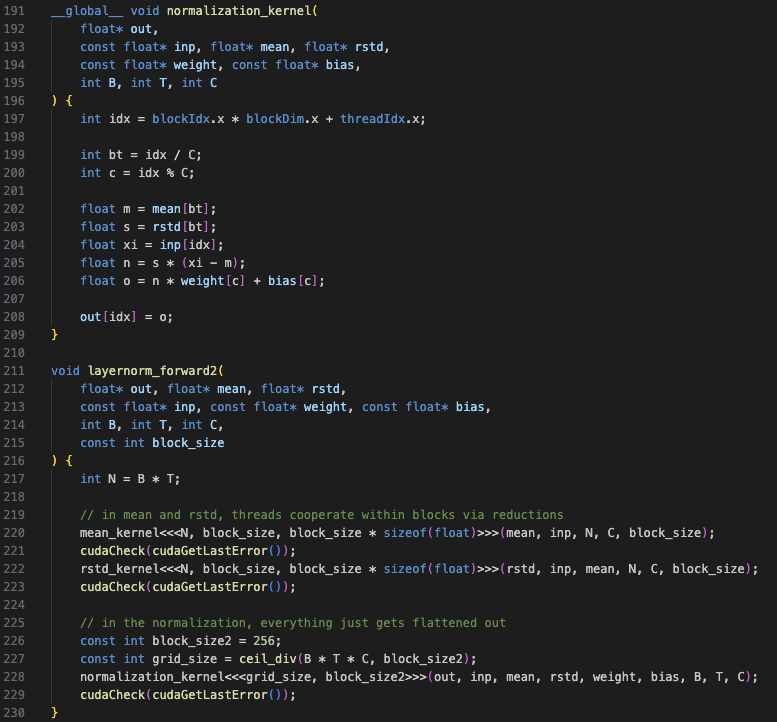
Kernel 2
In Kernel 2, steps 1, 2 and 3 are implemented as separate kernels. For the mean and rstd kernels, each block is responsible for one segment of C instead of each thread (see Figure-2a) which allows for further parallelization. Whereas for the normalization kernel (step 3), each thread calculates one output element.
Since both the mean and rstd calculations involve the sum operation, they make use of thread coarsening and reduction. In thread coarsening, each thread sums corresponding elements and stores it in a shared memory array (same size as the thread block). In reduction, the elements in the shared array are iteratively reduced to obtain the final sum. For more details, see the thread coarsening and reduction pocket references.
These optimizations lead to an improvement of ~5x over Kernel 1 (for block size 512).

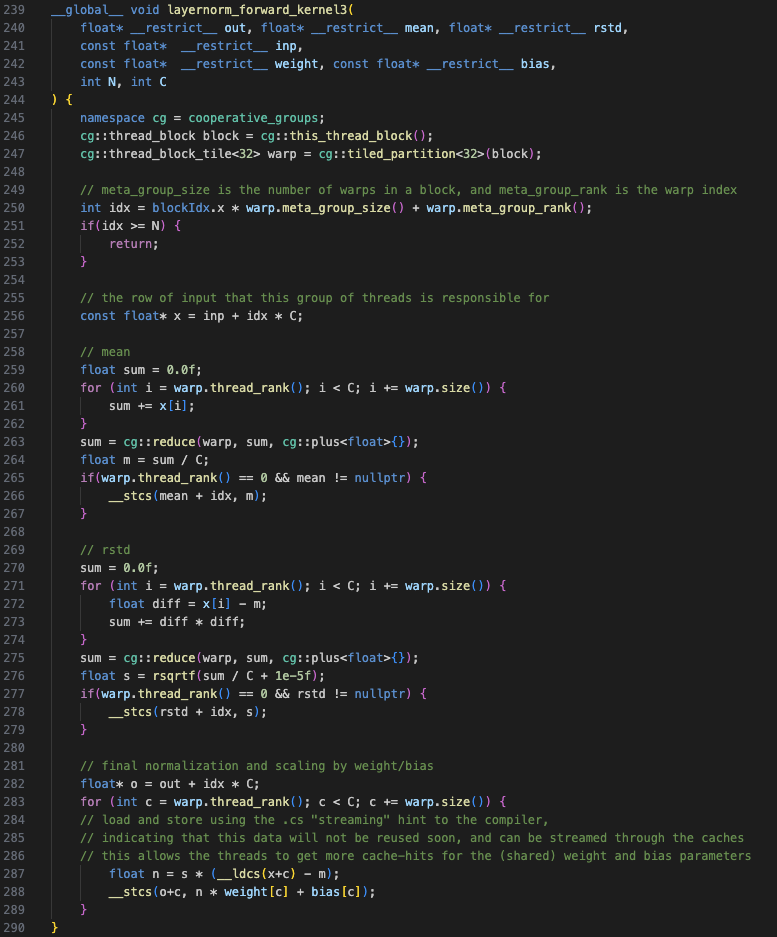
Kernel 3
Kernel 3 introduces the use of cooperative groups, allowing us to utilize
thread groups of arbitrary sizes (multiples of 2) that are not limited to the thread
block. The cooperative groups concept provides thread group classes
(tiled_partition<N>(g)) with useful methods such as thread_rank(),
which returns the id of the current thread in that group (similar to
threadId.x), and reduce(), which performs a reduction operation
(similar to that described in Figure-2a) on the values assigned to variables for
threads in that group. The cooperative groups objects are defined within the
cooperative_groups namespace.
This kernel uses a thread group (or tile) size of 32 to align with the number of threads in a warp (let's refer to this thread group as a warp). Hence, one warp is responsible for one segment of C in Kernel 3 (see Figure-3a - A warp of size 4 is used for simplicity). Also note that all operations are again combined in a single kernel.
This kernel also includes a few additional changes:
- Use of the `restrict` keyword: This allows the compiler to perform further optimizations through reduced memory accesses and computation.
- Use of Cache Operators:
__stcs()and__ldcs()limit cache pollution.
These optimizations lead to an improvement of ~1.8x over Kernel 2 (for block size 512).

Kernel 4
This kernel is similar to Kernel 3, except for the formula used to calculate variance. The variance is calculated as follows, leading to fewer subtraction operations:
$$Var[x] = \mathbb{E}[x^2] - (\mathbb{E}[x])^2$$
This simple change also leads to a small improvement of ~1.2x over Kernel 3 (for block size 512).
Kernel 5
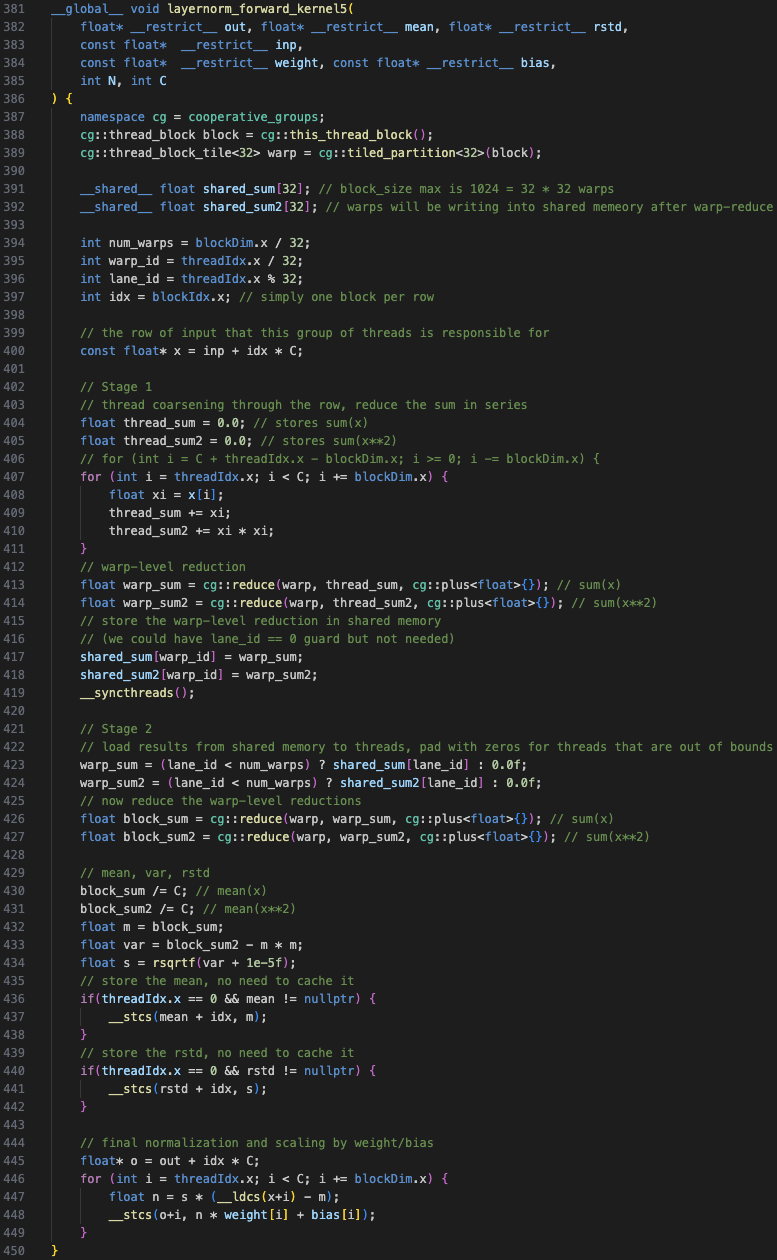
The final kernel operates in two stages. Similar to Kernel 2, each block is responsible for one segment of C. In stage 1, even though thread coarsening is done on the block level, the first reduction is done on the warp level. This sum is written into a shared memory array whose size is equal to the number of warps. In stage 2, the threads in the first warp are re-used to perform another warp reduction on the shared array to obtain the final sum. There is no thread coarsening for this stage. See Figure-4a for the complete flow.
The final kernel improves by ~1.25x over Kernel 4 and ~13x over the first kernel (for block size 512).

Summary
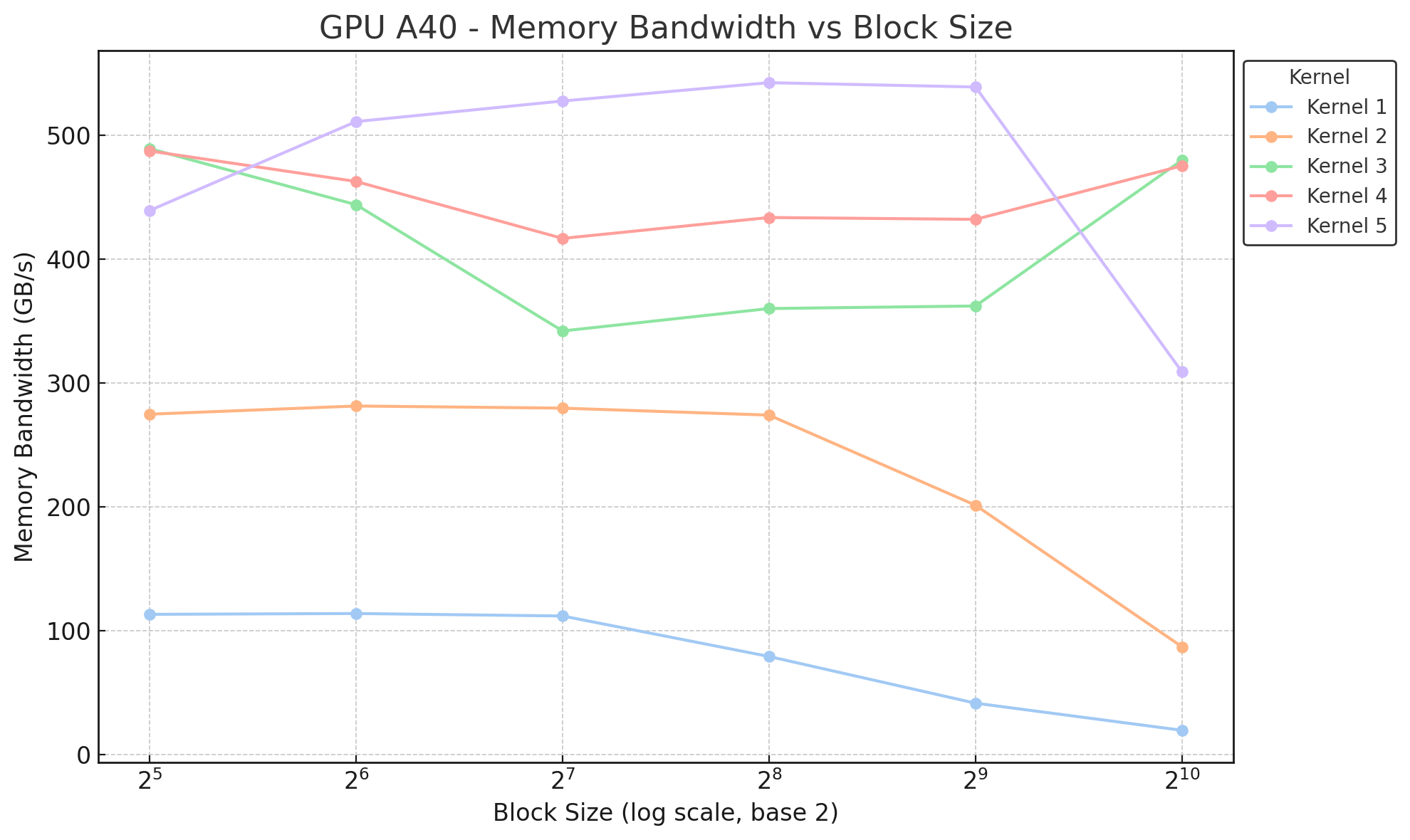
The following figure provides a summary of the memory bandwidth for all kernels on a A40 GPU across different block sizes:
References and Useful Links
- Code for LayerNorm forward kernels from the llm.c github repository
- Layer Normalization paper
- CUDA C++ Programming Guide
- CUDA Parallel Thread Execution (PTX) Guide



